
MODELADO DIDÁCTICO PARA DIDÁCTICAS ESPECÍFICAS: CIENCIAS COMPUTACIONALES
Manuela Cabezas[1]
Este artículo discute un enfoque y área de investigación en didáctica específica desde el análisis de una propuesta de investigación interdisciplinaria. Desde el estudio de la introducción del paradigma de las ciencias computacionales en Ciencias Físicas, Matemáticas e Informática, se introducen algunos conceptos y métodos vinculados al modelado didáctico centrado en teoría. Más específicamente, los avances de investigación presentados en este artículo se refieren una propuesta de modelado didáctico en el marco del proyecto de investigación “El paradigma de las ciencias computacionales y la educación” que se viene desarrollando desde inicios del 2022 y reúne un equipo interdisciplinario de investigadores y docentes de educación media en Ciencias Físicas, Matemáticas e Informática.
¿Qué cambios, para qué y cómo?
El proyecto de investigación “El paradigma
de las ciencias computacionales y la educación” propone abordar, desde el
modelado didáctico, una serie de desafíos ya planteados hace más de 40 años
(ver Papert, 1980), que siguen vigentes al día de hoy (Cabezas, 2021): ¿qué
aspectos de las ciencias de la computación debemos introducir en la educación y
de qué forma? Este desafío surge desde el reconocimiento de que la computación
ha producido transformaciones tanto cuantitativas como cualitativas en el mundo
(Denning & Tedre, 2019) y que esta realidad debe verse reflejada en la
educación (Papert, 1980; Atkin & Black, 1996; Wing, 2006). En este sentido,
los logros del pasado han sido
insuficientes y, en algunos casos, directamente contraproducentes (Cuban 1992;
Papert 1993; Dowek, 2005; Wilson et al., 2010; CECE, 2017).
En revisiones bibliográficas vemos un área de conocimiento muy dinámica, con gran diversidad en conceptos, métodos y enfoques, así como en nuevas áreas propuestas para la investigación (Malmi et al. 2014). Sin embargo, la informática y la programación como contenido educativo continúa produciendo cierta confusión sobre qué enseñar y cómo (Cansu & Cansu 2019; Barr & Stephenson, 2011; Pears, Tedre, Valtonen, y Vartiainen, 2021b).
Existe también, desde hace años, una preocupación por lograr establecer un grado de integración disciplinar, no solamente en cuanto a las prácticas de enseñanza, sino también para la construcción de bases epistemológicas y la validación empírica del conocimiento didáctico (ver Pears et al., 2007; da Rosa & Gómez, 2019). Una integración disciplinar es necesaria para lograr una introducción exitosa de la disciplina en el sistema educativo (Fensham, 2004).
En el campo de las investigaciones en
educación, la integración es una problemática reconocida que radica en la
difícil relación teoría - práctica, investigación - profesión y, por último,
didáctica general - específica (Korthagen et al., 2001; Fensham, 2004; Krogh et
al, 2021). Una de las soluciones propuestas para superar el impasse viene del
campo de estudios didácticos y propone la participación activa de docentes y
maestros en la construcción del conocimiento que constituye la base científica
de sus prácticas (Runesson,2011). Al contrario de la conceptualización del
profesional docente/maestro como consumidor/implementador de conocimientos
científicos, las investigaciones didácticas
integran al docente/maestro como agente esencial para la correcta
formulación/análisis de preguntas y enfoques en el modelado didáctico
(Runesson, 2011; Lunde & Sjöström, 2021).
Es así que surge la actual investigación, partiendo del modelo epistemológico y las experiencias de investigación y formación docente del núcleo interdisciplinario (Instituto de Computación de la Facultad de Ingeniería de UDELAR, ANEP y PEDECIBA área Informática) (ver da Rosa & Gómez, 2020), así como otros caminos recorridos en áreas de didácticas específicas (Stigler & Hiebert, 1999; Gu et al., 2004; Lijnse, 2001).
El modelado didáctico: de lo general a lo específico
Las corrientes que analizan el problema de
la enseñanza son múltiples y mejor entendidas como “historically evolved forms
of reflection within the social system” (Hopmann, 2015). Las didácticas
específicas están ligadas al estatus de la didáctica como campo de
investigación dentro de las disciplinas académicas de la educación, así como la
noción de la didáctica como disciplina científica propia (ver Mason 1998a;
Fensham, 2004; Krogh et al, 2021). Se postulan como campo de investigación
entre la teoría y la práctica, que se ocupa de describir y comprender en el
proceso de enseñanza y el aprendizaje de un contenido específico, para llegar a
interpretarlo en términos de “teoría didáctica” (Lijnse, 2001; ver también,
Marton, 2015). Entendido así, Lijnse (2001) define las teorías didácticas como
teorías que participan en la construcción de soluciones concretas y modelos
didácticos que, en este caso, aplicamos para introducir las ideas fundamentales
de la computación en la enseñanza de Ciencias
Físicas e Informática en educación media. El modelado didáctico es el proceso
por el cual producimos las teorías didácticas basado en la metodología
denominada “Learning Study” (estudio de aprendizaje) (Runesson, 2011; Marton,
2015).
En un Learning Study se diseñan secuencias
didácticas que permiten al estudiante experimentar diferentes aspectos del
fenómeno/objeto a estudiar (Ling Lo, 2012). Al tener oportunidad de
experimentar múltiples variaciones durante el período en que se familiarizan
con el objeto (van resolviendo problemas, respondiendo preguntas, describiendo
su vivencia) pasan por un proceso en el que van encontrando ciertos patrones
(lo que se mantiene invariante, lo que cambia, la relación entre las partes,
etc.). Marton (2015) parte de las ideas de Mulhall (1993) para estudiar este
proceso de detección de patrones que permite discernir los “aspectos críticos”
del objeto de aprendizaje y, de tal forma, formular
respuestas/soluciones/estrategias exitosas ante problemas nuevos o contextos no
predeterminados (Marton, 2015, p.22). Hablamos de “teoría de la variación” por
el rol de la diferenciación en el proceso de discernir los aspectos críticos en
un objeto específico (Ling Lo, 2012). El aspecto crítico es una propiedad del
objeto, que no resulta intuitivo para el estudiante desde sus conocimientos
previos y requiere un periodo de experimentar variación y discernir en ella
ciertos patrones que aportan a la toma de conciencia sobre dicho objeto
(Marton, 2015). Al introducir un nuevo objeto, podemos ayudar al estudiante a
discernir lo que queremos enseñar presentando variación el objeto. Por ejemplo,
utilizando ejemplos donde sus aspectos críticos cambian (para presentar
lo que No es) y ejemplos en los que cambian aspectos no críticos (ejemplos
varios de lo que sí es). A este patrón le llamamos “contraste” donde, por
ejemplo, para discernir el objeto “verde”, presentamos el concepto “color” como
aspecto crítico.
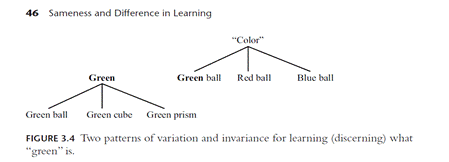 |
Figura 1
Nota: La figura presenta un ejemplo de variación y permanencia para presentar el color verde. Fuente: Marton, F. (2015). Necessary conditions of learning. Routledge.
El aspecto crítico, color, es presentado en
dos patrones, en uno varía y en el otro permanece incambiante. Este proceso
permite la separación del objeto, o sea, distinguir sus propiedades y
límites (cuándo deja de ser verde). Existen otros dos patrones en la teoría de
la variación relacionados al contraste: la generalización y la fusión. La
generalización viene después de la separación y sucede cuando el contraste de
“color” (ver figura 1, caso superior derecho) es usado para abstraer, del caso
específico al general. Una vez introducido el contraste, la propia reflexión
del/la estudiante puede generar la generalización. Alternativamente, puede ser
un proceso guiado, a través de acciones didácticas como ser preguntas de reflexión,
discusión, etc. Mediante el contraste, buscamos los aspectos necesarios del
objeto de aprendizaje, los que lo definen. El foco está en ellos y una vez que
los/las estudiantes pueden identificarlos hemos tenido éxito. Con la
generalización, queremos separar los aspectos secundarios de los aspectos
necesarios logrando manejar todos los elementos del objeto, entendiendo sus
partes. Por último, es necesario lograr la reintegración del objeto: El patrón
llamado fusión define la relación entre dos (o más) aspectos por medio de su
variación en simultáneo (Marton, 2015, p.51).
Si miramos el ejemplo del color verde, buscamos que los/las estudiantes generalizar los dos aspectos (necesarios y secundarios) de forma independiente: cualquier color puede aparecer con cualquier forma (Marton, 2015).
Modelado didáctico para un Learning Study
Partiendo del modelo epistemológico desarrollados sobre la construcción de conocimiento algoritmos, estructuras de datos y programas, enmarcados en la Epistemología Genética de Jean Piaget (da Rosa & Gómez, 2020), diseñamos el proyecto de investigación didáctica para el modelado de ciertos contenidos específicos de Ciencias Físicas e Informática en Secundaria y UTU.
El equipo directivo está conformado por tres investigadores en informática del InCo, dos docentes de ANEP (Matemática e informática), un docente del departamento de filosofía de la Facultad de Humanidades y Ciencias de la Educación y quien escribe. Para el modelado didáctico el equipo de trabajo está constituido por cinco docentes de educación media: tres de Informática y dos de Ciencias Físicas con al menos un grupo de estudiantes a su cargo que participan del proceso.
El trabajo se orientó en dos direcciones:
por un lado, el grupo de investigadores en informática estudió bibliografía
sobre las ideas fundamentales en computación que articulan el
conocimiento básico necesario para la didáctica de las ciencias
computacionales. Por otro lado, el grupo de docentes de ANEP y quien escribe,
elaboraron la planificación del modelado didáctico para realizar los ciclos de
investigaciones de aula, en las que las ideas fundamentales son estudiadas en
un Learning Study. Se realizaron reuniones de trabajo para la elaboración de
varios documentos guía para la recolección de datos y se participó de congresos
para la difusión de avances[1].
Hoy en día, el proyecto inicia la recolección de datos que es realizada durante las clases de Informática y Ciencias Físicas en instituciones de secundaria y UTU y consiste en grabaciones de audio y video, además de los propios materiales de producción de los estudiantes como parte de las actividades de las secuencias (cuestionarios, diagramas de Frayer, etc.). La recolección de datos es parte del ciclo completo de modelado didáctico, de acuerdo a la figura 2: Figura 2
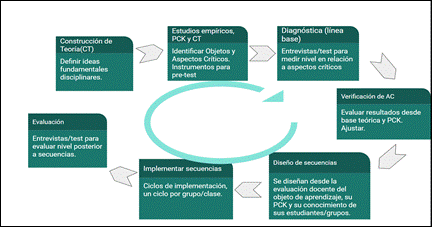
Nota: La figura muestra el ciclo de diseño, implementación y revisión/análisis de las secuencias didácticas. Fuente: creación propia.
Previo a la implementación de las
secuencias didácticas se realiza un estudio diagnóstico (individual) para
identificar los conocimientos previos de los estudiantes (sobre el objeto de
aprendizaje). El estudio de evaluación de acuerdo a
instrumentos de estudio previo (actividad/entrevista) eventualmente con
ajustes. La propuesta incluye un período para definir las ideas fundamentales
(Schwill, 1997) como parte esencial del proceso de integración disciplinar. Las
ideas seleccionadas son:
1. La información se representa en forma digital.
2. Los algoritmos interactúan con los datos para resolver problemas computacionales.
3. El rendimiento de los algoritmos se puede modelar y evaluar.
Para cada una de ellas se identificaron objetos de aprendizaje y sus aspectos críticos desde las experiencias y el conocimiento del equipo sobre qué aspectos implican mayor dificultad (detectado por estudiantes vs docentes). Se identificaron y definieron a priori los aspectos críticos que queremos que los estudiantes logren discernir, partiendo de las tres etapas del modelo epistemológico vinculados a las ideas fundamentales disciplinares (ver da Rosa & Gómez, 2020).
Por ejemplo, en torno al concepto de función que, si bien es trabajado en Ciencias Físicas y Matemáticas, requiere el trabajo previo de las ideas fundamentales para introducirlo como concepto computacional.
Cada idea tiene a su vez relación con los aspectos a considerar:
Componentes - datos de entrada, datos de salida (información/problema).
Relación entre ellos - función de una entrada en una salida (de información a algoritmo).
Expresión - la expresión de la función (solución).
Ejecución - programa que funciona (de algoritmo a programa).
Con ese objetivo se realiza el diseño de las secuencias didácticas, permitiendo que los/las estudiantes experimenten contraste, generalización y fusión en la introducción del objeto función. En las secuencias variamos sistemáticamente ciertos aspectos mientras otros son constantes para que puedan discernir el objeto entre otros objetos, sus partes en relación al todo y sus bordes/límites (la diferencia entre el objeto y el contexto y otros objetos relacionados). Gu et al. (2004), por ejemplo, discute el proceso de variación en el procedimiento de resolución de problemas (en este caso, matemáticos), y propone que la variación deriva de tres formas de resolver problemas: podemos extender el problema original cambiando ciertas condiciones del problema, cambiando los resultados y la generalización. También podemos introducir múltiples métodos que llegan a solucionar el problema cambiando los procedimientos de resolución y asociándolos a distintos métodos. Por último, introducir ejemplos dentro de un grupo de problemas similares, pero significativamente diferentes, utilizando el mismo método para experimentar sus aplicaciones. En este caso, se distingue la variación de lo conceptual de lo procedimental, ambos aspectos necesarios para incluir en la experimentación de variación aspectos necesarios y secundarios en torno a los contenidos estudiados en nuestra investigación. Durante el corriente año se están diseñando todas las secuencias e implementando en aulas en todos los grupos, pasando luego al ciclo de análisis colaborativo.
Es importante resaltar la palabra
colaborativo en relación al ciclo posterior a las experiencias de aula,
recordando que en la propuesta de Learning Study, la participación de los
docentes como agentes esenciales de la investigación son lo que distinguen este
enfoque, de otros similares. La meta es la construcción de teorías didácticas
con la participación activa de quienes la van a aplicar. El principal aporte de
las experiencias de investigación es el resultado de la experiencia en los
propios investigadores/docentes, en primer lugar y, en segundo lugar, el
impacto que tienen en su entorno (Mason, 1998b).
Referencias
Atkin, J. M. & Black, P. J., (Eds.). (1996). Changing the subject: Innovations in science, mathematics and technology education. Taylor & Francis.
Barr, V., & Stephenson, C. (2011). Bringing computational thinking to K-12: What is involved and what is the role of the computer science education community?. Acm Inroads, 2(1), 48-54.
Cabezas, M. (2021). Pensamiento Computacional, Educación STEM y la Educación Informática. Revista Sudamericana de Educación, Universidad y Sociedad, 9(1), 45-59.
Cansu, S. K. y Cansu, F. K. (2019). An overview of computational thinking. Journal ofComputer Science Education in Schools, 3(1).
CECE. (2017). The Committee on European Computing Education (CECE) yAssociation for Computing Machinery (ACM) Informatics Education in Europe:Are We All En The Same Boat? New York NY United States, doi:10.1145/3106077.
Cuban, L. (1992). Managing Dilemmas While. Building Professional Communities. Educational researcher, 21(1), 4-11.
da Rosa, S., & F. Gomez. (2019, September). Towards a research model in programming didactics. In 2019 XLV Latin American Computing Conference (CLEI) (pp. 1-8). IEEE.
da Rosa, S., & Gómez, F. (2020). A research model in didactics of programming. CLEI ELECTRONIC JOURNAL, 23(1).
Denning, P. y Tedre, M. (2019). Computational thinking. Cambridge, MA: The MITPress.
Denning, P., y Tedre, M. (2021). Computational thinking: A disciplinaryperspective. Informatics in Education, 20(3), 361–390.https://doi:10.15388/infedu.2021.21
Fensham, P. J. (2004). Defining an identity: The evolution of science education as a field of research, Kluwer Academic Publisher.
Gu, L., Huang, R., & Marton, F. (2004). Teaching with variation: A Chinese way of promoting effective Mathematics learning. In L. Fan, N. Y. Wong, J. Cai & S. Li (Eds.), How Chinese learn Mathematics: Perspectives from insiders. Singapore: World Scientific Publishing.
Korthagen, F.A., Kessels, J., Koster, B., Lagerwerf, B. y Wubbels, T. (2001). Link-ing practice and theory: The pedagogy of realistic teacher education. Mahwah: Rout-ledge.
Krogh, E., Qvortrup, A., & Graf, S. T. (2021). Introduction: Didaktik and curriculum in ongoing dialogue. In Didaktik and curriculum in ongoing dialogue (pp. 1-21). Routledge.
Hopmann, S. (2015). ‘Didaktik meets Curriculum’revisited: historical encounters, systematic experience, empirical limits. Nordic Journal of Studies in Educational Policy, 2015(1), 27007.
Ling Lo, M. (2012). Variation theory and the improvement of teaching and learning. Göteborg: Acta Universitatis Gothoburgensis.
Lijnse, P. (2001). Didactics of science: the forgotten dimension in science education research?. Designing theory-based teaching-learning sequences for science education, Proceedings of the symposium in honour of Piet Lijnse at the time of his retirement as Professor of Physics Didactics at Utrecht University. ISBN: 978-90-73346-70-3
Lunde, T., & Sjöström, J. (2021). Didaktiska modeller som kärnan i ämnesdidaktik: forskning som eftersträvar en professionsvetenskap för lärare. ATENA didaktik, 3(1).
Malmi, L., Sheard, J., Bednarik, B., Helminen, J., Kinnunen, P., Korhonen, A.,Myller, N., Sorva, J., Taherkhani, A., Simon, (2014). Theoretical underpinnings of computing education research: what is the evidence? ICER14: Proceedings of the tenthannual conference on International computing education research pp. 27–34.
Marton, F. (2015). Necessary conditions of learning. Routledge.
Mason, J. (1998a). Researching from the inside in mathematics education. Mathematics Education as a Research Domain: A Search for Identity: An ICMI Study Book 1. An ICMI Study Book 2, 357-377.
Mason, J. (1998b). Enabling teachers to be real teachers: Necessary levels of awareness and structure of attention. Journal of Mathematics Teacher Education, 1(3), 243-267.
Mulhall, S. (1993). On being in the world: Wittgenstein and Heidegger on seeing aspects. London, UK: Routledge.
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. BasicBooks.
Papert, S. (1993). The children's machine: Rethinking school in the age of the computer. New York.
Pears, A., Seidman, S., Malmi, L., Mannila, L., Adams, E., Bennedsen, J. & Paterson, J. (2007). A survey of literature on the teaching of introductory programming. Working group reports on ITiCSE on Innovation and technology, Computer Science Education, 204-223.
Pears, A., Tedre, M., Valtonen, T. y Vartiainen, H. (2021b). What makescomputational thinking so troublesome? doi:10.13140/RG.2.2.20480.35842
Runesson, U. (2011). Lärares kunskapsarbete–exemplet learning study. om undervisning och lärande, Stiftelsen SAF i samarbete med Lärarförbundet 6-17.
Schwill, A. (1997). Computer science education based on fundamental ideas. Information technology: supporting change through teacher education, 285-291.
Stigler, J.W. and Hiebert, J. (1999), The Teaching Gap: Best Ideas from the World’s Teachers for Improving Education in the Classroom, Summit Books, New York, NY.
Wilson, C., Sudol, L., Stephenson, C. y Stehlik, M. (2010). Running on empty:The failure to teach k12 computer science in the digital age. Association forComputing Machinery, ISBN 9781450388672.
Wing, J. (2006). Computational thinking. Communications of the ACM, 49(3)
2 Presentación en el Workshop Psychology of Programming Interest Group, PPIG 2022 y publicación en los anales del mismo del paper “The construction of knowledge about programs”, accesible en https://www.ppig.org/papers. Presentación en el Simposio Argentino de Educación en Informática (SAEI), perteneciente a las Jornadas Argentinas de Informática (JAIIO 2022), y publicación en las memorias de las JAIIO del artículo “Modelado didáctico para ideas fundamentales de computación”, (accesible en https://publicaciones.sadio.org.ar/index.php/JAIIO/issue/view/38).